布隆过滤算法总结

背景

在数据处理中，我们经常有这样的需求，判断某个元素是否在一个指定集合中。最朴素的处理方法是首先存储指定集合中数据，然后查找集合中数据，如有数据和查找元素相等即归属于该集合。

在数学中，如果只利用集合的定义属性，查找只能通过穷举遍历。如果集合元素较大，势必会影响查找的性能。

这时候对于集合数据类型使用特殊的数据架构实现，这就是Hash表（散列表）。集合数据结构由三个部分组成：

数据坐标集合B。
原始数据集合A。
Hash Function。hash函数是原始集合A到坐标集合的映射。

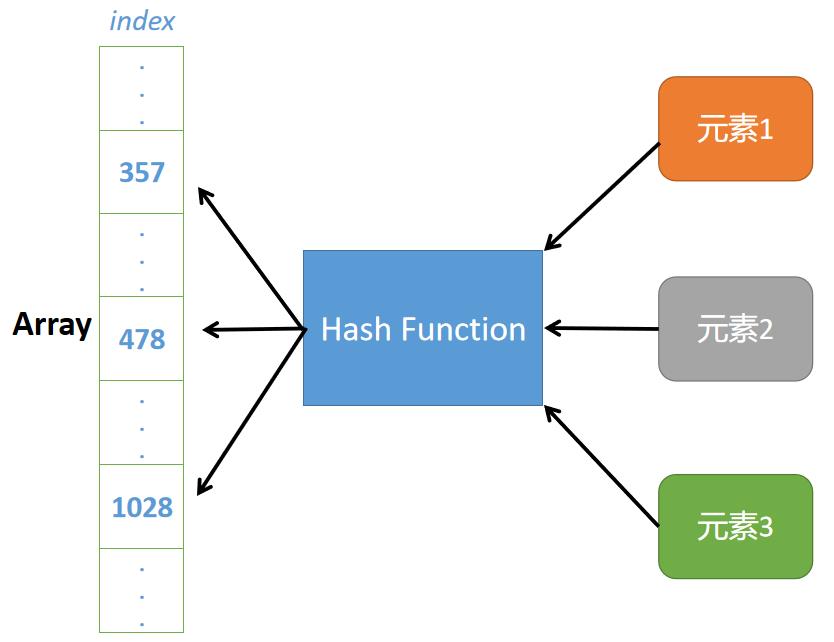
在这种数据结构下，判断元素是否属于指定集合，只需要计算该元素在hash函数作用下的坐标值。而这个坐标设置为数组的坐标，通过数组坐标就可以获取这个地址空间存储的值，最后判断是否和元素相等。

上面是最朴素的原理，在实际中由于hash函数的特点，存在集合A中不同值在hash函数映射下，坐标值可能是相同的，这就是hash冲突。具体细节后续介绍。

Hash表的实现本质思想是“空间换取时间”，对于特别大的集合，这种换取需要海量的内存存储空间。例如经常列举的案例就是垃圾邮件过滤场景。

引用自吴军的《数学之美》。Yahoo, Hotmail 和 Gmail 等公众电子邮件提供商，需要过滤垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的存储。如果用哈希表，每存储一亿个 email 地址，就需要 1.6 GB 的内存（用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6 GB内存资源）。因此存储几十亿个邮件地址可能需要上百 GB 的内存。

那么我们重新分析一下我们业务场景，实际核心需求是：判断元素是否重复，并不需要存储集合中具体数据。

数据坐标集合B，在数学中我们有很多实现方式（空间坐标等）。但是在计算机科学中，我们需要使用基础数据结构和运算方式。布隆（Burton Howard Bloom）在1970年提出布隆过滤器算法，算法中使用位阵列（Bit Array）作为坐标集合。接下来我们将详细介绍。

第一部分 Hash函数

1.1 Hash函数定义

Hash函数，通常音译为哈希函数（也有翻译成：散列函数）。Hash函数首先是数学意义上的函数：
$$
Hash\ Function\ F：A->B
$$
其中定义域集合A是不等长的字符串集合，而值域集合B中字符串是固定长度。

理论上满足这样的函数的海量的，我们在挑选好的Hash函数时，通常有下面的标准：

Hash函数在计算值域的时候是高效的（对于长度为n的字符串计算时间复杂度应为O(n)）。
确定性。对于任何给定的输入，哈希函数必须始终给出相同的结果。即函数值的确定性。
Hash碰撞概率低。由于值域集合中字符串是固定长度的，那么肯定是一个有限集合。例如SHA256算法值域大小（集合的势）为2^256。在我们进行2^256+1次输入时，必然会发生一次碰撞（$$x!=y,F(x)=F(y)$$）。所以选取的Hash函数针对具体场景，需要具有较低的碰撞概率。
隐蔽性。通俗的讲就是不能通过函数值F(x)，反向计算出x。这就是计算理论和密码学中单向函数概念。由于这个特性Hash函数大量应用于加密场景。
值域集合分布均匀。谈到分布那么值域空间就引入了距离的概念。通俗的讲就是点与点之间打散在空间中，没有聚集现象。

Hash函数将一个空间A中的数据映射到另一个空间B（坐标空间）中数据，通常集合B小于集合A（集合的势）。数据空间A定义成Hash表，在数据初始化和插入过程需要计算Hash坐标，并存储。这就完成了将计算时间（或计算消耗）转换成存储空间的思想。

1.2 Hash函数种类

通常按照Hash函数的实现原理分为：加法Hash、位运算Hash、乘法Hash、除法Hash、查表Hash、混合Hash。

1.2.1 加法Hash

Hash将字符串字符相加并处理后形成结果。下面案例同余质数。

public static void main(String[] args) {
    System.out.println(additiveHash("Secure Hash Algorit",19));
    // 输出3
}

public static int additiveHash(String key, int prime){
    int hash,i;
    for(hash=key.length(),i=0;i<key.length();i++){
        hash+=key.charAt(i);
    }
    return hash%prime;
}

1.2.2 位运算Hash

这类型Hash函数通过利用各种位运算（常见的是移位和异或等）来充分的变换输入元素。

public static void main(String[] args) {
    System.out.println(rotatingHash("Secure Hash Algorit",19));
    //6
}
public static int rotatingHash(String key,int prime){
    int hash,i;
    for(hash = key.length(),i=0;i<key.length();i++){
        hash=(hash<<1)^(hash>>10)^key.charAt(i)&key.charAt(i);
    }
    return hash%prime;
}

1.2.3 乘法Hash

这种类型的Hash函数利用了乘法的不相关性.

public static void main(String[] args) {
    System.out.println(bernstein("Secure Hash Algorit"));
    //361558494
}    
public static int bernstein(String key){
    int hash=0;
    int i;
    for(i=0;i<key.length();i++){
        hash=hash*10+key.charAt(i);
    }
    return hash;
}

1.2.4 除法Hash

因为除法太慢，这种方式几乎找不到真正的应用。

1.2.5 查表Hash

查表Hash中有名的例子有：Universal Hashing和Zobrist Hashing。他们的表格都是随机生成的。

1.2.6 混合Hash

混合Hash算法利用了以上各种方式。各种常见的Hash算法，比如MD5、Tiger都属于这个范围。它们一般很少在面向查找的Hash函数里面使用。

1.3 Hash函数应用

Hash函数主要应用有：

安全加密

密钥加密通常使用MD5和SHA系列算法。SHA系列有五个算法，分别是 SHA-1、SHA-224、SHA-256、SHA-384，和SHA-512。后四者有时并称为 SHA-2。SHA-1在许多安全协定中广为使用，包括 TLS/SSL 等，是 MD5 的后继者。

SHA-256可能是所有加密哈希函数中最著名的，因为它已在区块链技术中广泛使用。中本聪的原始比特币协议中使用了它。
唯一标识

文件之类的二进制数据做 md5 处理，作为唯一标识，这样判定重复文件的时候更快捷。
数据校验

比如从网上下载的很多文件（尤其是P2P站点资源），都会包含一个 MD5 值，用于校验下载数据的完整性，避免数据在中途被劫持篡改。
分布式缓存

分布式缓存和其他机器或数据库的分布式不一样，因为每台机器存放的缓存数据不一致，每当缓存机器扩容时，需要对缓存存放机器进行重新索引（或者部分重新索引），这里应用到的也是哈希算法的思想。
负载均衡

对于同一个客户端上的请求，尤其是已登录用户的请求，需要将其会话请求都路由到同一台机器，以保证数据的一致性，这可以借助哈希算法来实现，通过用户 ID 尾号对总机器数取模（取多少位可以根据机器数定），将结果值作为机器编号。

第二部分布隆过滤

2.1 原理

前文我们讨论了“判断某个元素是否在一个指定集合中”问题的实现思路。在数据量较小的情况下，我们可以使用经典的HashMap数据结构。对于大量数据场景下，布隆（Burton Howard Bloom）在1970年提出布隆过滤器算法。

2.2 Java实现

2.2 布隆过滤的应用

Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的IO次数［3］。

Squid 网页代理缓存服务器在 cache digests 中使用了也布隆过滤器［4］。

Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据［5］。

SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间［6］。

Google Chrome浏览器使用了布隆过滤器加速安全浏览服务［7］。

参考文献及资料

1、数学之美二十一：布隆过滤器（Bloom Filter）：http://www.google.com.hk/ggblog/googlechinablog/2007/07/bloom-filter_7469.html

目录

背景